平成28年度卒業研究紹介「中央値と順序統計量を求めるアルゴリズムの実験的評価」
発表者: 吉富 大佑(情報科学科)/指導教員: 朝廣 雄一 教授
順序統計量とは、配列の要素の中のk番目に小さい値のことである。順序統計量を求める方法として、配列をソートした後に添え字を使ってk番目に小さい値を探し出すというものがある。しかし、この方法では配列のデータを一度完全にソートする必要があるため配列のデータ数が増えるにつれて処理時間が非常に長くなる。そのため、順序統計量を効率的に探し出すためには順序統計量を求めるために工夫されたアルゴリズムを使う必要がある。
本研究では、順序統計量を求めるために工夫がされたアルゴリズムと配列をソートして順序統計量を求める方法の平均実行時間を比べ、どの程度の差があるのか実験的評価を行った。ソートアルゴリズムとしてバブルソート、選択ソート、挿入ソート、クイックソート、マージソートの5種類、順序統計量を求めるために工夫されたアルゴリズムとして、平均線形時間選択アルゴリズム、最悪線形時間選択アルゴリズムを実装し実験を行った。実験にはランダムに整数の要素を生成した要素数10000〜20000の配列を用いた。要素数を1000ずつ増やしていき、それぞれ250回ずつ実験を行いその平均実行時間を実験結果とした。
実験の結果、平均実行時間は早い順に平均線形時間選択アルゴリズム、クイックソートを利用したアルゴリズム、同程度の実行時間で最悪線形時間選択アルゴリズム、マージソートを利用したアルゴリズム、挿入ソートを利用したアルゴリズム、選択ソートを利用したアルゴリズム、バブルソートを利用したアルゴリズムとなった。平均線形時間選択アルゴリズムはアルゴリズムの工夫による高速化の例として非常にわかりやすいものとなった。最悪線形時間選択アルゴリズムの良さは本研究では明らかにならなかった。このアルゴリズムは最悪でもO(n)の実行時間を保証するものであるため、ランダムな配列を入力すると工夫の良さが十分に発揮されなかったと考えられる。工夫の良さを明らかにするには、他のアルゴリズムが苦手とする入力のデータを用意し、実行時間を比較する必要があると考えられる。
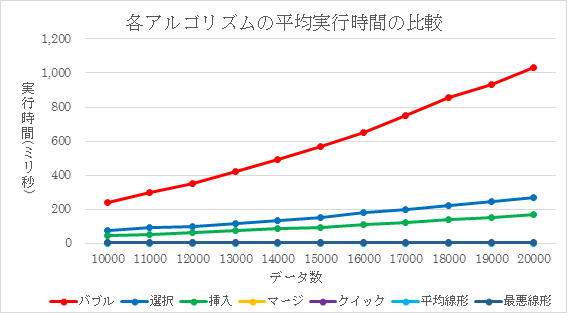
図1: 各アルゴリズムの平均実行時間(O(n2)のアルゴリズムを含む)
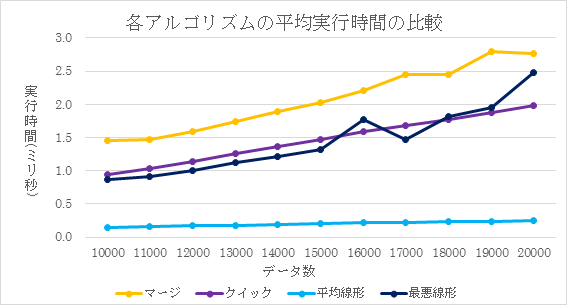
図2: 各アルゴリズムの平均実行時間(O(n2)のアルゴリズムを除く)
この卒業研究は平成28年度情報科学部優秀卒業研究に選出されました。
(2017/02/08 掲載。記載内容は執筆当時のものです)